Menjawab pertanyaan sang fisikawan terkemuka itu, matematika sebenarnya bisa dibuktikan dengan berbagai cara. Pembuktian tersebut meliputi pembuktian langsung, kontraposisi, kontradiksi, dan induksi matematika.
Lantas, bagaimana cara membuktikan matematika dengan empat jenis pembuktian tersebut? Dilansir dari Ruangguru, berikut masing-masing penjelasannya:
1. Pembuktian Langsung
Pembuktian langsung adalah metode pembuktian yang menggunakan alur maju, mulai dari pendefinisian sampai menghasilkan kesimpulan. Untuk menggunakan alur maju, maka pernyataan-pernyataan sebelumnya harus benar.Sebagai contoh, untuk membuktikan pernyataan “jumlah dari dua bilangan genap adalah bilangan genap”, maka rumuskan terlebih dahulu definisi dari bilangan genap itu sendiri. Umpamakan ada dua bilangan genap sembarang sebagai m dan n.
Dari definisi bilangan genap, m dan n dapat ditulis:
- m = 2k, dengan k adalah suatu bilangan bulat
- n = 2i, dengan i adalah suatu bilangan bulat
Manipulasi sedikit pernyataan tersebut agar bisa mendapat bentuk yang diinginkan. m + n = 2k + 2i bisa diubah menjadi 2 (k + i), dengan (k + i) juga bilangan bulat.
Setelah itu, lanjutkan ke kesimpulan. Kesimpulan ini harus berdasarkan pernyataan sebelumnya.
m + n dapat ditulis menjadi 2 kali suatu bilangan bulat (k + i). Sesuai definisi bilangan genap, maka m + n merupakan bilangan genap juga.
2. Kontraposisi
Kontraposisi merupakan salah satu metode pembuktian tidak langsung. Metode ini memanfaatkan prinsip logika matematika, yaitu: p → q ≡ ∼q → ∼p.
Artinya, kalau mau membuktikan ‘pernyataan p akan menghasilkan pernyataan q’ itu benar, maka buktikan saja ‘pernyataan bukan q maka menghasilkan bukan p’.
Sebagai contoh, untuk membuktikan pernyataan “bila n bilangan bulat dan 7n + 9 bilangan genap, maka n bilangan ganjil”, maka kategorikan dulu masing-masing pernyataan p dan q.
Pernyataan p adalah 7n + 9 bilangan genap, dan pernyataan q adalah n bilangan ganjil. Maka, yang dibuktikan adalah ‘bila n bukan bilangan ganjil (bilangan genap), maka 7n + 9 bukan bilangan genap (bilangan ganjil)’.
Selanjutnya, umpamakan n sebagai bilangan genap sembarang dengan pernyataan: n = 2k, dengan k bilangan bulat. Karena n = 2k, maka 7n + 9 bisa dituliskan menjadi:
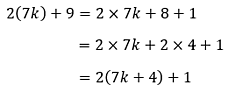
Pernyataan 7k + 4 sudah pasti merupakan bilangan bulat. Pernyataan ini bisa dimisalkan dengan m, sehingga: 2(7k) + 9 = 2m + 1, dengan m bilangan bulat. Sesuai definisi bilangan ganjil, maka 2(7k) + 9 atau 7n + 9 adalah bilangan ganjil.
Terbukti, bila n bukan bilangan ganjil, maka 7n + 9 juga bukan bilangan genap. Secara tidak langsung, dapat disimpulkan bahwa jika n bilangan bulat dan 7n + 9 bilangan genap, maka n bilangan ganjil.
3. Kontradiksi
Kontraposisi merupakan metode pembuktian tidak langsung. Metode ini memanfaatkan prinsip logika matematika, yaitu: jika p → q bernilai benar padahal q salah, maka p salah.
Sebagai contoh, untuk membuktikan pernyataan “bila n bilangan bulat dan n bilangan genap, maka 7n + 9 bilangan ganjil”, kategorikan dulu masing-masing pernyataan p dan q.
Pernyataan p adalah ‘n bilangan genap’, sedangkan pernyataan q ialah ‘7n + 9 adalah bilangan ganjil’. Buktikan pernyataan n bukan bilangan genap (bilangan ganjil). Dengan begitu, untuk ‘7n + 9 adalah bilangan ganjil’ benar akan muncul suatu kontradiksi.
Umpamakan bilangan ganjil sembarang n. Dari definisi bilangan ganjil, n dapat dinyatakan sebagai: n = 2k + 1, dengan k bilangan bulat. Karena n = 2k + 1, maka 7n + 9 dapat dituliskan menjadi:
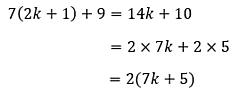
Kemudian, umpamakan 7k + 5 dengan m, sehingga: 7n + 9 = 14k + 10 = 2m. Pernyataan 14k + 10 atau 7n + 9 menyatakan bahwa nilainya 2 kali suatu bilangan bulat.
Padahal, itu merupakan definisi bilangan genap. Hal ini berkontradiksi dengan asumsi awal yang menyatakan 7n + 9 adalah bilangan ganjil. Itu artinya, asumsi awal n adalah bilangan ganjil, salah.
4. Induksi Matematika
Induksi matematika membuktikan suatu pernyataan untuk setiap bilangan asli. Metode ini terdiri dari tiga langkah.Pertama, buktikan bilangan awal dari sebuah pernyataan itu benar. Kemudian, asumsikan pernyataan benar tersebut untuk sembarang bilangan asli yang diumpamakan dengan k.
Terakhir, lakukan pembuktian untuk bilangan asli k + 1. Buktikan bahwa pernyataan tersebut juga benar.
Itulah empat metode yang bisa digunakan untuk membuktikan teori matematika. Jadi terbayang, bukan, betapa sulitnya ilmuwan mengemukakan sebuah teori? (Nurisma Rahmatika)
Baca: Belajar Matematika Lebih Asyik dan Mudah dengan Etnomatematika
Cek Berita dan Artikel yang lain di
Google News



















