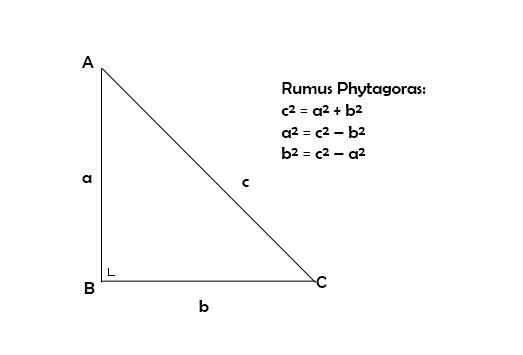
Seperti yang diketahui segitiga siku siku mempunyai sudut 90°. Adapun sisi terpanjangnya disebut dengan sisi miring atau hipotenusa. Sisi lainnya adalah alas dan tinggi.
Untuk mengukur salah satu sisi tersebut maka diperlukan teorema phytagoras. Berikut bunyi
teorema phytagoras:
"Sisi miring atau sisi terpanjang dalam segitiga siku–siku sama dengan kuadrat sisi-sisi lainnya."
Segitiga Siku Siku
Segitiga siku-siku adalah segitiga yang sudutnya membentuk sudut siku-siku yang memiliki jumlah derajat sebesar 90 derajat. Berikut cek sifat dari segitiga siku-siku:
- Segitiga siku siku memiliki dua sisi yang saling tegak lurus
- Segitiga siku siku memiliki satu sisi miring dan salah satu sudutnya adalah sudut siku siku atau 90°
- Segitiga siku siku tidak memiliki simetri putar dan simetri lipat.
| Baca juga: Rumus Luas Segitiga Siku Siku dan Kelilingnya |
Rumus Phytagoras

Rumus Phytagoras segitiga siku-siku. Foto: Pexels.
c² = a² + b²
Lalu, bagaimana cara untuk mencari sisi lainnya yaitu sisi depan dan sisi samping? Maka dengan demikian, rumusnya menjadi seperti berikut ini:
a² = c² – b² (mencari sisi depan)
b² = c² – a² (mencari sisi samping)
Perlu juga diketahui tentang pola triple phytagoras, dengan menghafalkan tripel pythagoras bisa lebih cepat menyelesaikan soal tanpa perlu menghitung. Di awal sudah dijelaskan bahwa ditemukan sebuah fakta pola segitiga dengan panjang sisi 3, 4, dan 5 satuan panjang akan membentuk segitiga siku siku.
Contoh soal
Soal 1
YouTuber Jerome Pollin beberapa waktu lalu membuat sebuah tantangan kepada para influencer dan konten kreator untuk menyelesaikan soal matematika. Salah satunya, menghitung sisi segitiga siku-siku. Berikut ini soalnya:Ada segitiga siku siku siku, panjang sisi miringnya adalah 15 cm, panjang salah satu sisi lainnya adalah 9 cm (mendatar), maka panjang sisi satunya lagi adalah?
Diketahui:
c: 15 cm (sisi miring)
b: 9 cm (sisi mendatar)
Ditanya:
Sisi tegak a?
Jawaban:
Karena yang dicari adalah sisi tegak maka rumus yang digunakan a² = c² – b².
a² = c² – b²
a² = 15² – 9²
a² = 225-81
a² = 144
a= √144
a= 12 cm
Jadi, sisi tegak (a) adalah 12 cm
Soal 2
Sebuah segitiga siku-siku memiliki sisi tegak 9 cm dan sisi depan 12 cm. Berapakah sisi miring dari segitiga siku-siku tersebut?Diketahui:
Sisi tegak (b) = 9 cm
Sisi depan (a) = 12 cm
Ditanya:
Sisi miring (c) = ?
Jawab:
c² = a² + b²
c² =12 ² + 9²
c² = 144 + 81
c² = 225
c = √225
c = 15 cm
Jadi, panjang sisi miring adalah 15cm
Soal 3
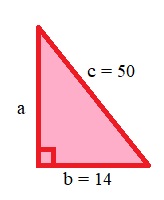
(soal Zenius)
Tentukan nilai a!
Pembahasan:
a2 = c2 – b2 = 502 – 142 = 2.500 – 196 = 2.304
a = √2.304 = 48
Jadi, nilai a adalah 48 cm.
| Baca juga: Rumus Mencari Luas dan Keliling Segitiga dan Contoh Soalnya |
Cek Berita terbaru dan Artikel menarik lainnya di Google News
Cek Berita dan Artikel yang lain di
Google News