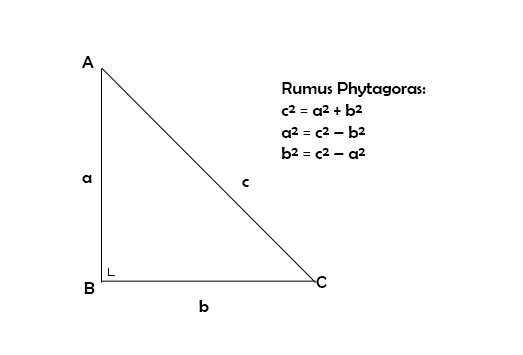
Untuk menyelesaikan soal seperti itu diperlukan rumus phytagoras. Rumus phytagoras digunakan untuk menghitung salah satu sisi dari segitiga siku-siku. Hal tersebut juga disampaikan Jerome ketika ada peserta tes yang tidak mengerti cara menyelesaikannya.
Sejarah teorema phytagoras
Rumus phytagoras diambil dari dari seorang filsuf Yunani asal Yunani Kuno, Pythagoras (570-495 SM). Dalam beberapa sumber dijelaskan bahwa teorema phytagoras sudah ada ketika orang Babilonia dan Cina menyadari suatu fakta bahwa segitiga dengan panjang sisi 3, 4, dan 5 satuan panjang akan membentuk segitiga siku siku (1900-1600 SM).
(Segita siku siku foto: Ist)
Bahkan jauh sebelum itu, teorema phytagoras juga disebutkan dalam Baudhayana Sulbasutra India yang ditulis antara 800 dan 400 SM tentang Tripel Phytagoras. Kemudian
teorema tersebut dikreditkan kepada Phytagoras.
Teorema phytagoras
Seperti yang diketahui segitiga siku siku mempunyai sudut 90°. Adapun sisi terpanjangnya disebut dengan sisi miring atau hipotenusa. Sisi lainnya adalah alas dan tinggi.Untuk mengukur salah satu sisi tersebut maka diperlukan teorema teorema phytagoras. Berikut bunyi teorema phytagoras:
"Sisi miring atau sisi terpanjang dalam segitiga siku–siku sama dengan kuadrat sisi – sisi lainnya."
Rumus Phytagoras
Berdasarkan teorema phytagoras diperoleh rumus sebagai berikut untuk mencari sisi miring atau terpanjang pada segitiga siku-siku:c² = a² + b²
Lalu, bagaimana cara untuk mencari sisi lainnya yaitu sisi depan dan sisi samping? Maka dengan demikian, rumusnya menjadi seperti berikut ini:
a² = c² – b² (mencari sisi depan)
b² = c² – a² (mencari sisi samping)
Perlu juga diketahui tentang pola triple phytagoras, dengan menghafalkan tripel pythagoras bisa lebih cepat menyelesaikan soal tanpa perlu menghitung. Di awal sudah dijelaskan bahwa ditemukan sebuah fakta pola segitiga dengan panjang sisi 3, 4, dan 5 satuan panjang akan membentuk segitiga siku siku.