Contoh Soal Vektor Kelas 10 Beserta Kunci Jawaban

Jakarta: Besaran yang memiliki arah dan besar biasanya dinyatakan dengan ruas garis berarah. Nah, ruas garis berarah inilah yang disebut vektor.
 
Dalam Matematika, vektor digunakan untuk menggambarkan berbagai hal yang melibatkan arah dan jarak, seperti kecepatan, gaya, hingga perpindahan suatu benda.
 
Di bidang koordinat Cartesius, vektor memiliki dua komponen, yaitu horizontal (sumbu X) dan vertikal (sumbu Y). Dengan mengetahui kedua komponen ini, vektor bisa digambar secara tepat dan besarnya (modulus) dapat dihitung dengan rumus matematika.

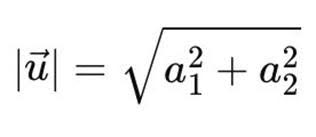
Perbedaan Vektor

Vektor bisa dibedakan berdasarkan sifat dan fungsinya:

1. Vektor posisi: menunjukkan posisi suatu titik, pangkal di titik O (0,0).
2. Vektor nol: besar nol dan tidak memiliki arah.
3. Vektor satuan: besar 1 satuan, digunakan untuk menunjukkan arah.
4. Vektor negatif: besarnya sama dengan vektor asal tapi arahnya berlawanan.
5. Vektor sama: memiliki besar dan arah identik, meski pangkalnya berbeda.

Operasi Vektor

Vektor tidak hanya punya besar dan arah, tapi juga bisa dioperasikan dengan mudah:

1. Perkalian dengan skalar

Mengalikan vektor 
 
membuat besar vektornya n kali lebih besar dan arah tetap sama.

2. Penjumlahan vektor

Bisa dilakukan dengan aturan segitiga (ujung vektor pertama ke pangkal vektor kedua) atau aturan jajargenjang (pangkal kedua vektor sama, resultan adalah diagonal jajargenjang).

3.  Selisih vektor

Artinya menjumlahkan vektor pertama dengan vektor negatif dari vektor kedua: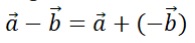
 

4. Vektor basis

 

Modulus dan jenis Vektor di Ruang

Modulus vektor adalah panjang vektor yang digambarkan sebagai segmen garis berarah. Untuk vektor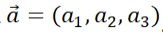  , besar vektornya: 
 
Vektor posisi menunjukkan letak suatu titik di ruang koordinat Cartesius, dengan pangkal di
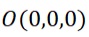 dan ujung di titik tertentu.

Jenis-jenis Vektor

Berikut jenis-jenis vektor yang perlu diketahui:

1. Vektor sama: besar dan arah identik.
2. Vektor negatif: besar sama tetapi arah berlawanan.
3. Vektor nol: besar nol, tanpa arah.
4. Vektor satuan: besar 1, menunjukkan arah; bisa dihitung dengan image.png.

Operasi dan perhitungan Vektor di Ruang

Vektor memiliki berbagai operasi yang penting untuk dipahami, baik dalam bidang datar maupun ruang tiga dimensi. Berikut penjelasannya:

1. Perkalian Vektor dengan Skalar

2. Penjumlahan dan Selisih Vektor

Penjumlahan vektor di ruang prinsipnya sama dengan di bidang datar. Selisih dua vektor artinya menjumlahkan vektor pertama dengan vektor negatif vektor kedua: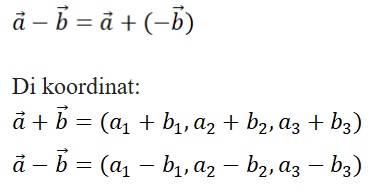
 

3. Titik Pembagi Garis

4. Perkalian Skalar (Dot Product)

Perkalian skalar antara dua vektor menghasilkan nilai skalar: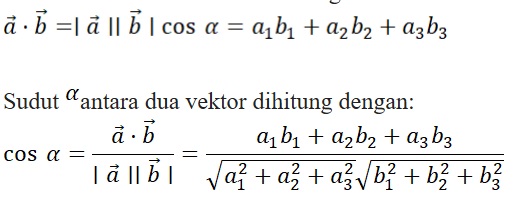
 

5. Proyeksi Vektor

 
Nah sekarang, simak beberapa contoh soal vektor Matematika Peminatan Kelas X berikut yuk. Ini bisa kamu jadikan latihan di rumah untuk menghadapi ujian.
   

Contoh soal latihan Vektor

Soal 1

Pada kubus ABCD.EFGH manakah diantara vektor berikut ini yang sama dengan ????????
 
A. ????????
B. ????????
C. ????????
D. ????????
E. ????F

Soal 2

Diketahui vektor ???? = 5i – 3j + 2k, maka panjang vektor ???? adalah ….
 
A. 3
B. 4
C. √20
D. 5
E. √38

Soal 3 

Diketahui |a|, |b|, dan |a – b| berturut-turut adalah 4, 6 dan 2 19 . Nilai |a + b| = ....
 
A. 4√19
B. √19
C. 4√7
D. 2√7
E. ½ √7

Soal 4 

Diketahui | → a | = √2 , | → b | = √9 , dan | → a + → b | = √5 Besar sudut antara vektor → a dan vektor → b adalah
 
A. 45° 
B. 60° 
C. 120° 
D. 135° 
E. 150° 

Soal 5 

Diketahui vektor ???? =3i − 4 j − 4k , ????⃗ = 2i − j + 3k , dan ???? = 4i − 3 j + 5k . Panjang proyeksi vektor (???? + ????⃗ ) pada ???? adalah….
 
A. 3√2
B. 4√2
C. 5√2
D. 6√2
E. 7√2

Soal 6 

Vektor a dan b vektor membentuk sudut a. Diketahui a = 6, b = 15, dan cos a = 0,7; maka nilai a ×(a + b ) = ....
 
A. 49
B. 89
C. 99
D. 109
E. 115

Soal 7 

Diketahui bahwa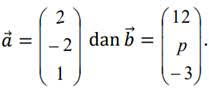
 

 
Jika kosinus sudut antara vektor ???? dan ????⃗ adalah 1/3, nilai p adalah....
 
A. 4 atau 24
B. −4 atau −24
C. 2 atau 14
D. −4 atau −12
E. −4 atau 14

Soal 8

Diketahui koordinat A(6, -2, -6), B(3, 4, 6) dan C(9, x, y). Jika titik-titik A, B dan C kolinear (segaris), maka nilai x – y sama dengan ....
 
A. –18
B. 4
C. 6
D. 10
E. 18

Kunci jawaban

1. C
2. E
3. D
4. D
5. B
6. C
7. A
8. D.

Semoga materi dan contoh soal ini bisa menambah pengetahuanmu yaa. (Syifa Putri Aulia)
 
Cek Berita dan Artikel yang lain di

Google News

Viral! 18 Kampus ternama memberikan beasiswa full sampai lulus untuk S1 dan S2 di Beasiswa OSC. Info lebih lengkap klik : osc.medcom.id