Turunan Fungsi Aljabar: Konsep, Rumus, dan Contoh Soal

Jakarta: Matematika memiliki beberapa macam konsep dan salah satunya adalah turunan fungsi aljabar. Konsep ini mulai dipelajari pada tingkat sekolah menengah. Penerapan dari fungsi turunan aljabar sendiri dapat ditemukan di kehidupan sehari-hari.

Apakah turunan fungsi aljabar?

Turunan fungsi aljabar merupakan materi yang erat kaitannya dengan limit fungsi dan gradien atau kemiringan garis. Turunan atau diferensial ini digunakan untuk menunjukkan perubahan gradien garis akibat perubahan nilai.
 
Secara sederhana, turunan fungsi di suatu titik adalah gradien garis singgung fungsi di titik tersebut. Untuk memahaminya lebih lanjut, simak penjelasan berikut yang dikutip dari laman Ruangguru.

Bagaimana konsep turunan fungsi aljabar?

Agar lebih mudah dipahami, coba perhatikan grafik fungsi berikut:
 


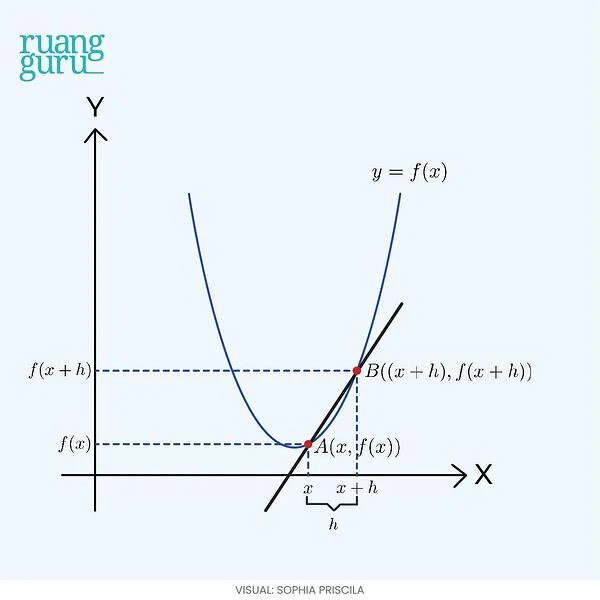
Gambar di atas merupakan grafik fungsi kontinu f(x) yang dipotong oleh sebuah garis lurus di dua titik, yaitu titik A dan B. Garis ini disebut sebagai garis secan atau garis AB.
 
Garis itu memiliki gradien tertentu berdasarkan letak absis (koordinat x) dan ordinat (koordinat y) masing-masing titik. Jika kedua titik tersebut digeser saling mendekati satu sama lain hingga jarak antartitiknya mendekati nol, maka kemiringan garis juga akan berubah.
 
Garis yang semula memotong kurva di dua titik akan berubah menjadi garis singgung yang tampak menyinggung kurva di satu titik saja. Karena jarak antartitik (h) mendekati nol, maka besarannya dapat diketahui menggunakan konsep limit dengan rumus sebagai berikut:
 

 
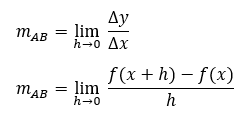
Nah, gradien garis singgung yang diperoleh dari rumus itulah yang disebut turunan fungsi.

Apa saja rumus turunan fungsi aljabar?

Secara umum, turunan fungsi aljabar dirumuskan sebagai berikut:
 

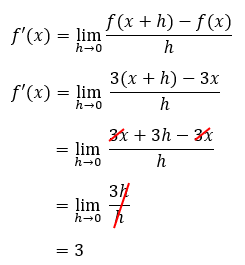
Rumus turunan fungsi pangkat

Namun, jika ditemukan soal fungsi pangkat, maka rumus yang bisa digunakan untuk mempermudah mencari turunannya adalah: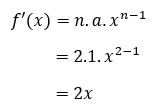
 

 
Keterangan:
 
n = angka pangkat
a = konstan

Rumus turunan fungsi komposisi

Selain itu, ada pula aturan rantai yang digunakan untuk mencari turunan fungsi komposisi. Bentuk fungsi tersebut adalah h(x) = f(g(x)). Adapun rumus turunannya sebagai berikut:
 
h’(x) = f’(g(x)).g’(x)

Rumus turunan fungsi pada operasi perkalian

Jika ditemukan soal fungsi berupa perkalian dengan bentuk f(x) = u(x).v(x), maka rumus turunannya adalah: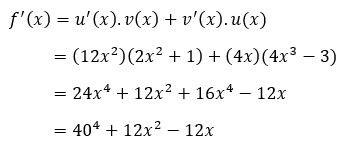
 

Rumus turunan fungsi pada operasi pembagian

Selai perkalian, ada pula fungsi berupa pembagian dengan bentuk f(x) = u(x) : v(x). Rumus untuk mencari turunan dari fungsi tersebut adalah: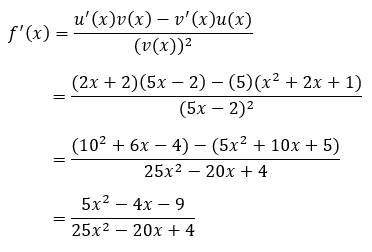
 

Baca juga: Mengenal 4 Rumus Turunan dalam Matematika & Fisika

Bagaimana contoh soal turunan fungsi aljabar?

Supaya lebih paham dengan materi di atas, perhatikan beberapa contoh soal berikut:

1. Turunan fungsi f(x) = 2 adalah…
   
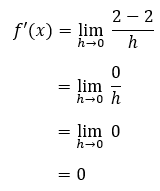
   Dengan kata lain, bisa dipastikan bahwa turunan fungsi konstan f(x) = C adalah selalu nol.
    
2. Turunan fungsi f(x) = 3x adalah…
   Pembahasan:
    
   
    
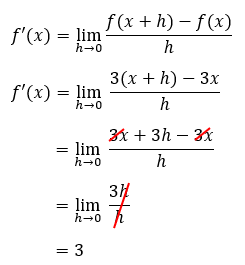
   Dengan kata lain, dapat disimpulkan bahwa turunan fungsi linear f(x) = ax ialah a, di mana a merupakan nilai konstan.
    
3. Turunan fungsi f(x) = x^2 adalah…
   Pembahasan:
   
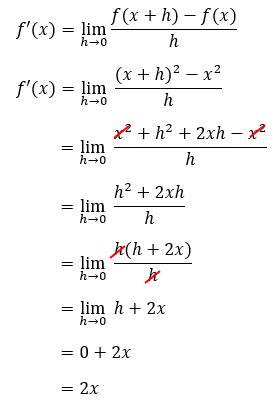
4. Turunan fungsi f(x) = (2x-4)^5 adalah…
   Pembahasan:
    
   Pertama, turunkan dulu fungsi luarnya, yaitu (2x-4)^5
    
   
    
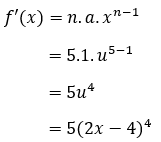
   Dari hasil tersebut, turunkan fungsi dalam kurung, yaitu 2x-4. Hasilnya adalah 2.
    
   Selanjutnya, hasil-hasil tersebut dimasukkan ke rumus turunan fungsi komposisi berikut:
    
   
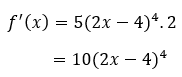
5. Turunan fungsi f(x) = (4x^3 - 3).(2x^2 + 1) adalah…
   Pembahasan:
    
   Pertama, hitung turunan dari masing-masing fungsi yang ada di dalam kurung.
   
    
   Selanjutnya, masukkan hasil tersebut ke rumus turunan fungsi pada operasi perkalian.
    
   
6. Turunan fungsi f(x) = (x^2 + 2x + 1) : (5x - 2) adalah…
   Pembahasan:
    
   Pertama, hitung turunan dari masing-masing fungsi yang ada di dalam kurung.  
    
   
    
   Selanjutnya, masukkan hasil tersebut ke rumus turunan fungsi pada operasi pembagian.
    
   

 

Bagaimana aplikasi turunan fungsi aljabar?

Dikutip dari Akupintar, turunan fungsi aljabar mempunyai empat jenis aplikasi. Apa saja aplikasi turunan fungsi aljabar?

1. Menentukan gradien garis singgung
   Turunan fungsi aljabar dapat digunakan untuk menentukan kemiringan atau gradien garis singgung (m) suatu kurva. Pada kurva dengan rumus y = f(x), gradien bisa dirumuskan sebagai: m = y' = f'(x).
2. Menentukan interval fungsi turun dan fungsi naik
   Turunan fungsi aljabar dapat menentukan span fungsi dengan syarat tertentu. Pada fungsi naik, syarat span haruslah f'(x) > 0. Syarat span fungsi turun adalah f'(x) < 0.
3. Menentukan nilai stasioner
   Bila fungsi y = f(x) berlanjut dan diferensiabel di x = a serta f'(x) = 0, maka fungsi memiliki nilai stasioner di x = a. Jenis nilai stasioner dari fungsi y = f(x) ditentukan dengan turunan kedua, di mana dapat berupa nilai balik least, nilai balik maksimum, atau nilai belok.
4. Memecahkan soal limit dengan bentuk yang tak tentu
   Turunan fungsi aljabar bisa digunakan untuk menyelesaikan limit berbentuk tak tentu atau 0/0. Pada soal tersebut dapat digunakan turunan fungsi f(x) dan g(x) serta keduanya.
   Jika menggunakan turunan pertama sudah dapat dihasilkan bentuk tertentu, maka bentuk tersebut adalah penyelesaiannya. Jika dengan turunan pertama masih belum dihasilkan bentuk tak tentu, maka masing f(x) dan g(x) diturunkan lagi hingga memperoleh hasil berbentuk tertentu.

Demikianlah pembahasan mengenai turunan fungsi aljabar, mulai dari konsep, rumus, contoh soal, hingga aplikasinya. (Nurisma Rahmatika)
 
Cek Berita terbaru dan Artikel menarik lainnya di Google News
 
Cek Berita dan Artikel yang lain di

Google News