Nah, kali ini, Medcom akan mengupas tuntas mengenai materi fungsi dan relasi pada mata pelajaran matematika, khususnya mengenai fungsi komposisi, biar Sobat Medcom enggak lupa dengan pelajaran penting ini! Penasaran? Langsung baca artikel berikut ini!
Pengertian Fungsi Komposisi
Sebelum membahas lebih lanjut, Sobat Medcom harus mengetahui apa itu fungsi. Dilansir dari Quipper, fungsi merupakan hubungan satu-persatu antara daerah awal dengan daerah kawan. Rupanya, sebuah fungsi dapat digantikan atau disubstitusikan ke dalam fungsi lainnya yang mana gabungan fungsi-fungsi tersebut dapat disebut sebagai fungsi komposisi.Singkatnya, fungsi komposisi merupakan gabungan antara dua atau lebih fungsi yang nantinya akan membentuk fungsi baru.
Tentunya, Sobat Medcom pasti pernah mendengar kata Fungsi f(x) kan? Fungsi f(x) merupakan fungsi yang mana nilainya bergantung pada nilai x, contohnya f(x) = 3x + 9 = 12. Apabila nilai x = 1, maka nilai fungsi tersebut ialah 3(1) + 9 = 12.
Kasus ini berbeda jika x yang digunakan ternyata juga merupakan fungsi, contohnya x = g(x). Lalu, bagaimana ya cara mengerjakannya? Jangan panik! kalian tinggal mencoba untuk mensubstitusikan x = g(x) pada f(x) yang nantinya akan mendapatkan hasil f(g(x)) atau lebih sering ditulis dengan (f o g)(x).
Penulisan dari (f o g)(x) adalah tulisan fungsi kompoissi secara matematis. Sampai disini, Sobat Medcom sudah bisa membayangkannya kan?
Rumus Fungsi Komposisi
Perhatikan ilustrasi berikut ini!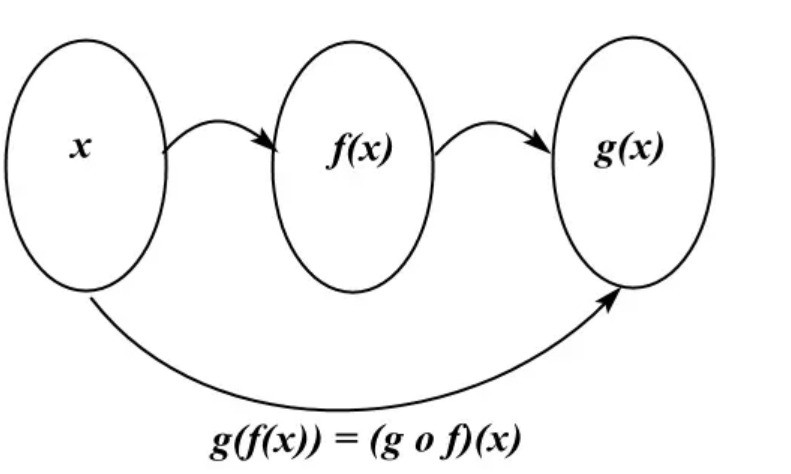
Foto: Dok. Quipper
Dalam diagram di atas, pemetaan derah asal – x, menunjukkan daerah kawan (range), yaitu f(x). Kemudian, pemetaan terjadi dari daerah kawan atau asal yang baru f(x) ke arah daerah kawan (range) yang kedua – g(x)
Sederhananya:
F:x → f(x)
f:f(x) → g(x)
Dari perumusan tersebut, maka dapat disimpulkan bahwa rumus fungsi komposisi ialah:
g o f = g(f(x))
f o g = f(g(x))
Syarat Fungsi Komposisi
Apabila dua buah fungsi ingin dikomposisikan, maka keduanya harus memenuhi syarat, yaitu irisan pada range – daerah kawan fungsi pertama dengan daerah asal fungsi kedua bukan himpunan kosong. Lebih jelasnya, wajib ada irisan antara range fungsi pertama dengan domain fungsi kedua yang mana jika ditulis dengan metode matematis, maka dapat dituliskan seperti berikut ini:R1 ⊆ D2 atau R1 ∩ D2 ≠ { }.
Biar lebih mengerti, kalian bisa memerhatikan contoh berikut ini!
F: {(1,5), (2,7), (3,9), (4,11)}
G: {(5,6), (7,12), (11,16)}
Dari kedua fungsi di atas, tentukan fungsi komposisi (f o g)(x) atau (g o f)(x)!
Seperti yang sudah dijelaskan sebelumnya, syarat dua fungsi untuk bisa dikomposisikan ialah R1 ∩ D2 ≠ { }.
Pertama, lihat dulu bagian fungsi (f o g)(x). Dari sini, kalian perlu menentukan daerah hasil g(x) dan daerah asal f(x). Dari sini, g(x) menjadi fungsi pertama dan f(x) merupakan daerah fungsi kedua.
Rg = {6, 12, 16}
Df = {1, 2, 3, 4}
Dari kedua himpunan di atas, bisa disimpulkan bahwa tidak ada irisan antara range fungsi g(x) dengan domain fungsi f(x). Oleh karena itu, (f o g)(x) tidak dapat didefinisikan atau tidak memenuhi syarat fungsi komposisi.
Kedua, lihat fungsi (g o f)(x).
Dalam hal ini, kalian dapat membuktikan hasil f(x) dengan daerah asal g(x). Disini, f(x) menjadi fungsi pertama denan g(x) menjadi fungsi kedua.
Rr= {5, 7, 9, 11}
Dg= {5, 7, 11}
Dari himpunan di atas, kalian berhasil memperoleh irisan atau Rr∩ Dg = {5, 7, 11}. Maka dari itu, kalian dapat menarik kesimpulan bahwa (g o f)(x) adalah fungsi komposisi. Dari sini, Sobat Medcom sudah mulai paham kan?
Sifat-sifat Fungsi Komposisi
Sebuah fungsi komposisi perlu memenuhi sifat-sifat berikut ini:Bersifat asosiatif – f o (g o h) = (f o g) o h. Sifat satu ini akan terpenuhi apabila Rh ∩ Dg ≠ { }; Rg ∩ Df ≠ { }.
Bersifat identitas – f o l = l o f
Dari kedua sifat di atas, apakah sifat komutatif merupakan salah satu sifat fungsi komposisi? Jawabannya, bukan ya, Sobat Medcom. Syarat-syarat di atas bertumpu pada penjelasan sebelumnya yang menyatakan (f o g) ≠ (g o f). Di catat ya!
Cara Mencari Fungsi Komposisi
Dalam mengetahui fungsi komposisi – baik (f o g)(x) maupun (g o f)(x) bisa dikategorikan cukup mudah. Kalian tinggal mensubstitusikan persamaan fungsi pertama dengan fungsi kedua. Seperti, untuk memperoleh (f o g), kalian bisa mensubstitusikan fungsi g(x) ke persamaan fungsi f(x). Perhatikan soal berikut ini!Diketahui:
f(x) = x + 4
g(x) = 3x + 6
Untuk mencari tahu persamaan fungsi (f o g)(x), kalian dapat mengetahuinya dengan mensubstitusikan g(x) = 3x - 6 ke f(x) = x + 4, seperti:
(f o g)(x) = f(3x-6) = 3x - 6 +4
(f o g)(x) = 3x - 2
Persamaan fungsi komposiis untuk (g o f)(x) dapat diketahui dengan mensubstitusikan f(x) = x +4 ke g(x) = 3x - 6 dengan:
(g o f)(x) = g(x+4) = 3(x+ 4) - 6
(g o f)(x) = 3x + 6
Lantas, bagaimana kasusnya kalau kalian diminta untuk menentukan fungsi f(x) atau g(x)? Mudahnya, kalian tinggal mencari tahu invers fungsi seperti ini:
Diketahui:
(f o g)(x) = 3x - 2
g(x) = 3x - 6
Berapakah persamaan fungsi f(x)?
(f o g)(x) = 3x - 2
(f(g(x)) = 3x - 2
f(3x - 6) = 3x - 2
Selanjutnya, tentukan invers dari g(x) atau g-1(x).
g(x) = 3x - 6 – misalkan g(x) = y, maka:
Y = 3x - 6
Y + 6 = 3x
X = y + 6/3
Kemudian, substitusikan nilai x = y + 6/3 ke dalam persamaan f(3x - 6) = 3x - 2
f(y) = 3(y + 6/3) - 2
f(y) = y + 4
f(x) = x + 4
Contoh Fungsi Komposisi
Sebenarnya, terdapat berbagai contoh dari fungsi komposisi, diantaranya:Diketahui:
f(x) = 2x + 4
g(x) = 3x + 2
h(x) = 5x - 1
Tentukan fungsi dari komposisi (f o g o h)(x)!
Cara pertama, kalian harus mengetahui persamaan untuk fungsi komposisi (g o h)(x).
g(x) = 3x + 2
h(x) = 5x - 1
(g o h)(x) = 3(5x - 1) + 2
= 15x - 1
Kemudian, tentukan (f o g o h)(x).
(f o g o h)(x) = f(g(h(x)))
= f(15x-1)
= 2(15x-1) - 4
= 30x - 6
Mudah kan?
Pengaplikasian Fungsi Komposisi
Teori fungsi komposisi ternyata dapat digunakan untuk membantu kehidupan sehari-hari lho Sobat Medcom! Di antaranya:Membantu memperhitungkan gaji serta tunjangan
Ketika seseorang yang merupakan PNS mendapatkan gaji pokok per bulan disertai tunjangan kinerja dengan tunjangan kesehatan, maka untuk memudahkannya dalam menghitung ketiga hal tersebut. Ia bisa mengaplikasikan rumus fungsi komposisi, lho Sobat Medcom.
Mengetahui pembelahan bakteri yang melibatkan dua besaran
Sobat Medcom pasti tahu kan bahwa pembelahan bakteri tidak terjadi dikarenakan satu faktor saja. Nah, untuk memudahkan para peneliti untuk mengetahui pembelahan tersebut, maka mereka harus bisa merumuskan fungsi komposisi yang melibatkan sejumlah besaran variabel seperti suhu dan waktu pembelahan bakteri.
Memecahkan permasalahan nilai tukar antar mata uang
Sebenarnya memang tidak memerlukan fungsi komposisi dalam memecahkan permasalahan nilai tukar unag. Namun, pastinya ada satu masa di mana kalian akan menukarkan dua tingkat mata uang.
Contohnya, ketika WNA menukarkan mata uang euro ke rupiah namun di tempat lain, ia berada di situasi dimana ia harus menukarkan kembali rupiah ke AUD. Dalam hal ini, perhitungan dua tingkat penukaran mata uang rupanya melibatkan fungsi komposisi dalam mengetahui nilai tukar kedua mata uang tersebut.
Contoh Soal serta Pembahasan Fungsi Komposisi
Biar Sobat Medcom semakin paham mengenai fungsi komposisi, coba kerjakan soal-soal berikut ini yuk!Tentukan daerah hasil dari fungsi komposisi (f o g)(x) dengan f(x) = 8 - x2 dan
Pembahasan:
Pertama, ketahui dahulu (f o g)(x)
(f o g)(x) = f(g(x))
= 8 - (g(x))2
= 8 - (√2-x)2
= 8 - (2-x)
= x + 6
Dari hasil perhitungan di atas, maka dapat disimpulkan bahwa (f o g)(x) = x + 6 ialah fungsi linear – himpunan domain tidak ada batasnya atau tidsak hingga. Apabila ditulis dengan matematis, maka menjadi {y| – ∞
Seorang ilmuwan tengah meneliti jejak tumpahan minyak di laut. Tiap satuan waktunya, jari-jari tumpahan minyak tersebut diketahui sebagai r(t) = 5t - t2. Selain itu, luas tumpahan minyak memiliki fungsi luas L(r) = πr2. Cari tahu bentuk persamaan luas tumpahan minyak tersebut tiap satuan waktunya!
Pembahasan:
Diketahui:
r(t) = 5t - t2
L(r) = πr2
Pertanyaan: L(t) = ..?
Hal yang perlu kalian lakukan pertama adalah untuk mengetahui (L o rr) atau fungsi waktu.
r(t) = 5t - t2
Kemudian, substitusikan nilai tersebut ke dalam persamaan luas.
L(r) = πr2
L(5t - t2) = π(5t - t2)2
L(t) = π(5t - t2)2.
Dari perhitungan di atas maka dapat disimpulkan bahwa L(t) = π(5t - t2)2.
Dalam sebuah industri terbagi atas dua tahapan proses produksi. Tahapan pertama merupakan proses penggilingan kedelai (x dalam kuintal) kemudian menjadi bubur kedelai (p dalam kuintal) dengan bantuan mesin A dan mengikuti fungsi p = f(x) = 2x2 + x - 5.
Selanjutnya, pada tahap kedua berlangsung pada mesin B dengan pengolahan bubur kedelai menjadi tahu dengan menggunakan persamaan fungsi g(p) = 2p - 15. Apabila kedelai yang tersedia untuk satu kali produksi seberat 5 kuintal, tentukan banyaknya tahu yang dihasilkan!
Pembahasan:
Hal pertama yang dapat kalian lakukan adalah menentukan jumlah hasil produksi pada tahap I di mesin A. Dalam tahapan ini, variabel x digunakan sebagai bahan baku dasar berupa kedelai utuh.
f(x) = 2x2 + x - 5
f(5) = 2(5)2 - 5 + 5
= 50.
Selanjutnya, substitusikan nilai f(5) dalam persamaan produksi tahap II di mesin B.
g(50) = 2(50) - 15
= 85 kuintal.
Sehingga, dapat disimpulkan bahwa jumlah tahu yang didapatkan tersebut adalah 85 kuintal.
Nah itu dia tadi pembahasan mengenai fungsi komposisi. Bagi Sobat Medcom yang ingin belajar lebih banyak mengenai matematika, jangan lupa untuk terus mengikuti kanal Pendidikan Medcom.id, ya! (Gracia Anggellica)
?
| Baca juga: Belajar Matematika: Menghitung Kemiringan atau Gradien |
Cek Berita dan Artikel yang lain di
Google News