Belajar Matematika: Menghitung Kemiringan atau Gradien

Jakarta: Sobat Medcom tahu enggak sih pesawat membutuhkan kemiringan tertentu untuk bisa lepas landas di udara atau mendarat di landasan pacu dengan sempurna? Tentunya, kemiringan tersebut melibatkan perhitungan matematika, lho!
 
Kali ini, kita akan belajar mengenai kemiringan pada sebuah garis lurus alias gradien, dilansir dari situs Ruangguru. Penasaran? Langsung simak artikel berikut!

Apa itu Gradien?

Secara umum, gradien dapat didefinisikan sebagai suatu nilai yang menunjukkan kemiringan pada suatu garis lurus dan biasanya disimbolkan dengan huruf “m”. Suatu garis gradien dapat miring ke berbagai arah tergantung nilai komponen X dan Y-nya.
 
Contohnya seperti ilustrasi berikut:


 
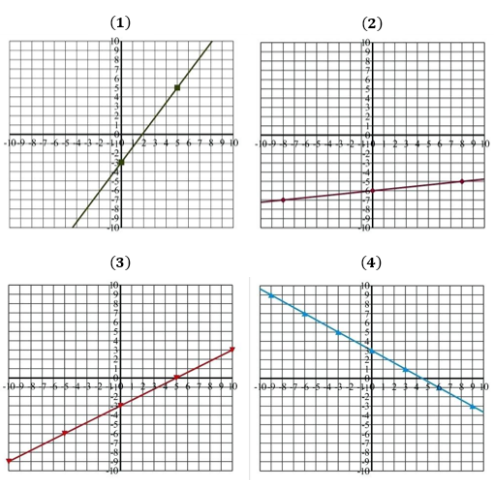
Tidak hanya itu saja, sebuah garis gradien positif akan miring ke arah kanan. Sementara itu, garis gradien negatif akan miring ke arah kiri. Kira-kira siapa ya yang menemukan teori kemiringan garis ini?

Penemu kemiringan garis (Gradien)

Rene Descartes adalah seorang matematikawan kelahiran Prancis, 31 Maret 1596. Selain berprofesi sebagai matematikawan, Rene juga merupakan seorang ilmuwan dan filsuf yang berhasil mengungkapkan sebuah metode dalam memecahkan kemiringan garis pada aljabar geometri.
 
Salah satu karya terbesarnya ialah Discourse on Method yang diperuntukkan untuk pengembangan dunia pendidikan. Setelah mengenal mengenai gradien serta penemunya, lalu bagaimana ya caranya agar kita bisa mencari nilai dari suatu gradien?

Cara mencari tahu nilai gradien

Terdapat dua cara untuk mengetahui nilai gradien pada sebuah garis, yakni

1. Apabila bentuk persamaan garisnya diketahui

Secara harafiah, terdapat dua macam bentuk persamaan garis lurus. Oleh karena itu, untuk mengetahui gradiennya juga berbeda-beda tergantung bentuk persamaan garisnya.

A. Persamaan garis y = mx + c

Persamaan garis satu ini lebih mudah dicari lantaran koefisien dari variabel x merupakan gradiennya.
 
Contoh soal:
 
1. Garis y = 3x + 2
 
Penyelesaian: koefisien x adalah 3, maka gradien dari garis tersebut adalah 3.
 
2. Garis y = -2x + 8
 
Penyelesaian: koefisien x adalah -2, sehingga gradien dari garis tersebut ialah -2.

B. Persamaan garis ax + by + c = 0

Apabila persamaan garis yang diketahui seperti di atas, maka langkah pertama yang harus kalian lakukan adalah mengubah persamaan garis ke bentuk y = mx + c, dengan m sebagai gradien garis tersebut. Kalian harus jelih dalam melihat tanda +/- pada koefisien tiap variabel lantaran simbol tersebut akan berubah apabila mereka dipindah ruas persamaannya.  
 
Contoh soal:
 
1. Hitunglah kemiringan pada persamaan garis berikut!
5x + 2y - 8 = 0
 
Penyelesaian:
 
Pertama, ubah persamaan 5x + 2y - 8 = 0 menjadi bentuk y = mx + c, maka persamaan tersebut menjadi 2y = -5y + 8. Koefisien pada x dan konstanta berubah tanda lantaran mereka dipindah ruas ke kanan.
 
2. Hitunglah kemiringan pada persamaan garis berikut!
2x - 3y = 7
 
Penyelesaian:
Y = (-5/2)x + 4
Sehingga persamaan gradien atau x dari soal B adalah -5/2.

2. Apabila dua titik yang dilalui garis diketahui

Jika hal yang diketahui adalah dua titik yang dilalui suatu garis lurus, contohnya (x1,y1) dan (x2y2), maka gradien akan didapatkan dari rumus m = ?y/?x = (y2-y1)/(x2-x1).
 
Contoh soal:
 

 
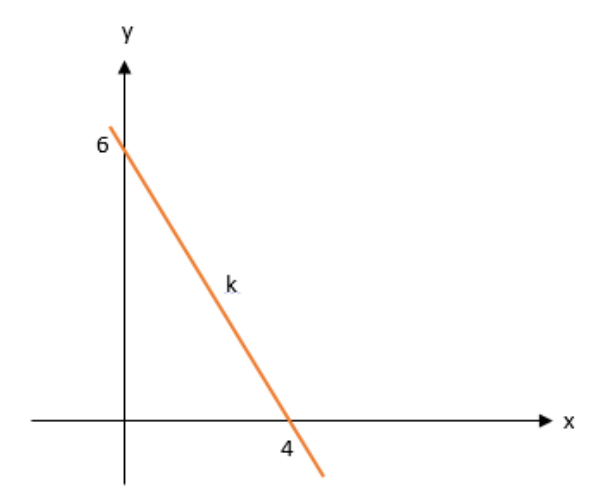
Berapakah gradien pada garis k?
 
Penyelesaian:
 
Diketahui, dua titik yang dilalui garis k, yakni (4,0) dan (0,6). Apabila kalian memilih (x1,y1) = (4,0) dan (x2y2) adalah (0,6), maka untuk mencari gradien tersebut dapat menggunakan rumus m = ?y/?x = (y2-y1)/(x2-x1).
 

 
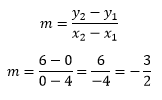
Sehingga, berdasarkan perhitungan di atas, maka gradien garis dalam ilustrasi di atas ialah -3/2. Sebenarnya kalian bebas memilih titik mana yang akan kalian jadikan (x1,y1) lantaran hasilnya akan sama saja.
 
Wah ternyata mudah banget ya untuk mencari kemiringan pada suatu garis! Untuk lebih memudahkan kalian dalam memahami rumus-rumus di atas, berikut rangkuman rumus untuk mencari kemiringan garis atau gradien.
 

 
Meski sudah dirangkumin, namun kalian tidak boleh hanya mengingat rumusnya saja, namun kalian juga perlu memahami konsep kemiringan garis, ya! Lantas, apa sih sebenarnya kaitan antara dua garis lurus? Untuk selengkapnya, kalian bisa melihat ilustrasi berikut!
 

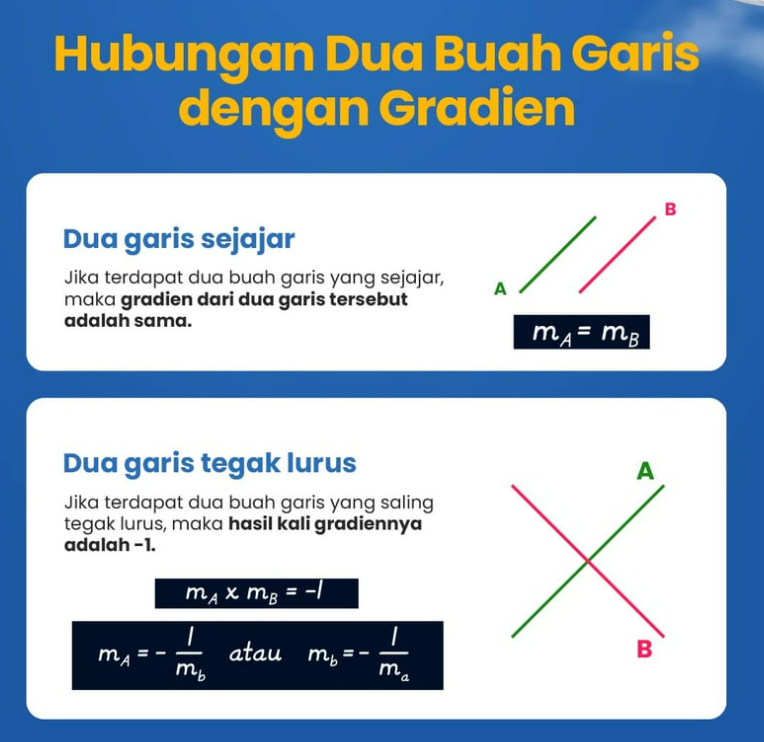
Nah itu dia tadi materi mengenai kemiringan atau gradien pada garis lurus matematika. Bagi Sobat Medcom yang ingin belajar lebih banyak mengenai matematika atau mengenal serba-serbi pendidikan lainnya, jangan lupa untuk terus ikuti Medcom, ya! (Gracia Anggellica)
 

Baca juga: Belajar Mengenai Rumus Luas Bangun Datar Yuk!

 
Cek Berita dan Artikel yang lain di

Google News