Belajar Matematika: Pengertian Statistika Deskriptif, Jenis, dan Contoh

Jakarta: Penelitian tak terlepas dari data. Umumnya, data yang diperoleh lebih dari satu. Semakin banyak data yang diperoleh, semakin besar pula peluang mendapatkan hasil yang sesuai.
 
Sebelum dilaporkan, data tersebut harus diolah dalam bentuk tabel atau grafik. Serangkaian proses mulai pengumpulan data, pengolahan, hingga penyajian ini dipelajari dalam statistika deskriptif. Apa yang dimaksud statistika deskriptif? Yuk simak penjelasannya dikutip dari laman Quipper:

Pengertian Statistika Deskriptif

Statistika deskriptif adalah ilmu pengetahuan yang mempelajari tentang cara mendapatkan, mengolah, serta menyajikan suatu data penelitian. Pada statistika, kamu akan diajak meringkas serta menyajikan suatu data dalam bentuk tabel, grafik, maupun histogram.
 
Selanjutnya, dari tabel atau grafik itu, kamu bisa menentukan simpangan rata-rata, rata-rata (mean), modus, median, dan sebagainya.

Pengertian Statistika Deskriptif menurut ahli

1. Sugiyono, yaitu analisis yang dilakukan untuk mengetahui keberadaan variabel mandiri, baik hanya pada satu variabel atau lebih tanpa membuat perbandingan variabel itu sendiri dan mencari hubungan dengan variabel lain
2. Iqbal Hasan, yaitu bagian dari statistika yang mempelajari tentang cara pengumpulan data dan penyajian data sehingga mudah dipahami
3. Bambang Suryoatmono, yaitu statistika yang menggunakan data pada suatu kelompok untuk menjelaskan atau menarik kesimpulan tentang kelompok itu saja

Tujuan Statistika Deskriptif

1. Memudahkan proses analisis data guna penarikan kesimpulan
2. Memberikan gambaran umum sebaran data
3. Memberikan gambaran umum variabel di dalam penelitian

Perbedaan Statistika Deskriptif dan Statistika Inferensial

Perbedaannya adalah statistika deskriptif hanya mencakup pada bagaimana data itu diolah sehingga lebih mudah untuk dipahami. Itu artinya, statistika deskriptif belum bisa digunakan untuk menarik kesimpulan, sedangkan statistika inferensial mencakup penarikan kesimpulan dari keseluruhan data.

Jenis Statistika Deskriptif

Jenis statistika deskriptif dibagi menjadi tiga, yaitu penyajian data, pemusatan data, dan penyebaran data. Apa perbedaan antara ketiga jenis tersebut?

1. Penyajian data

Penyajian data adalah kegiatan menampilkan data mentah hasil penelitian agar lebih mudah dipahami. Penyajian data bisa dilakukan dalam bentuk tabel distribusi frekuensi dan grafik.

Tabel distribusi frekuensi
 
Tabel distribusi frekuensi dibagi menjadi dua, yaitu tabel distribusi frekuensi data tunggal dan tabel distribusi frekuensi data berkelompok. Berikut contoh perbedaan kedua tabel tersebut.
 
A. Tabel distribusi frekuensi data tunggal
 
Untuk membuat tabel distribusi frekuensi data tunggal cenderung lebih mudah daripada data berkelompok. Kamu hanya perlu memasukkan data yang dimaksud beserta frekuensinya. Perhatikan contoh statistika deskriptif berikut.
 
Data perolehan nilai Matematika siswa SMA Taruna Jaya adalah sebagai berikut:
 
        9 8 7 6 9 9 8 7 8 8
        9 7 7 7 8 8 9 8 6 6
        8 7 8 8 9 6 6 9 7 7
 
Jika data-data tersebut dimasukkan dalam tabel frekuensi data tunggal akan menjadi:
 

 
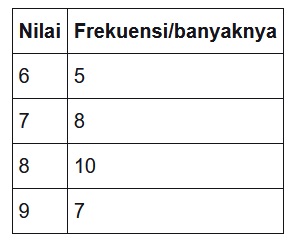
B. Tabel distribusi frekuensi data berkelompok
 
Tabel distribusi frekuensi data berkelompok adalah tabel yang datanya dibagi ke dalam interval kelas tertentu. Tabel ini lebih efektif digunakan untuk menyajikan data yang jumlahnya banyak, misalnya 100 data. Adapun langkah-langkah untuk membuat tabel frekuensi data berkelompok adalah sebagai berikut:

1. Menentukan daerah jangkauan (R), misal data terbesar 80 dan data terkecilnya 75 berarti jangkauannya 5
2. Menentukan banyak kelompok kelas dengan persamaan K= 1 + 3,3 log n dengan n= banyaknya data
3. Membuat interval kelas dengan persamaan
4. Menentukan batas atas dan batas bawah kelas
5. Menentukan tepi atas dan tepi bawah kelas

Perhatikan contoh berikut:
 
Berikut ini merupakan data berat badan siswa SMK Harapan Maju jurusan TKR A!
 
        45 46 45 50 55 47 48 46 50 51
        44 46 46 47 48 44 50 51 50 50
        44 45 45 45 46 47 50 51 50 51
        46 47 48 49 48 52 52 53 55 51
        45 50 51 55 47 48 46 55 52 46
 
Pembahasan:
 
Mula-mula, tentukan range atau jangkauan dari data tersebut:
 
Data terbesar = 55
Data terkecil = 44
R = 55 – 44 = 11
 
Banyak kelompok kelas
K = 1 + 3,3 logn
=  1 + 3,3 log50
= 1 + 3,3 (1,699)
= 6,6 ≈ 6 (jika diambil 7, jumlah interval tidak memenuhi banyaknya kelas)
 
Interval kelas
 

 
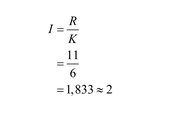
Dengan demikian, interval kelasnya 44 – 45, 46 – 47, 48 – 49, 50 – 51, 52 – 53, 54 – 55.
 
Apabila dinyatakan dalam bentuk tabel frekuensi data berkelompok, menjadi seperti berikut:
 
Diagram
 
Diagram adalah bentuk penyajian data dalam bentuk dua dimensi, misalnya diagram batang dan diagram lingkaran. Perhatikan data pada tabel nilai Matematika siswa kelas XA SMA Taruna Jaya seperti poin a berikut:
 

 
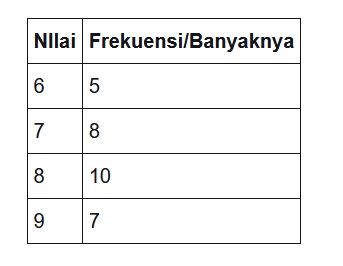
Jika data pada tabel berikut dijadikan diagram batang dan lingkaran akan menjadi seperti berikut:
 
Diagram batang
 

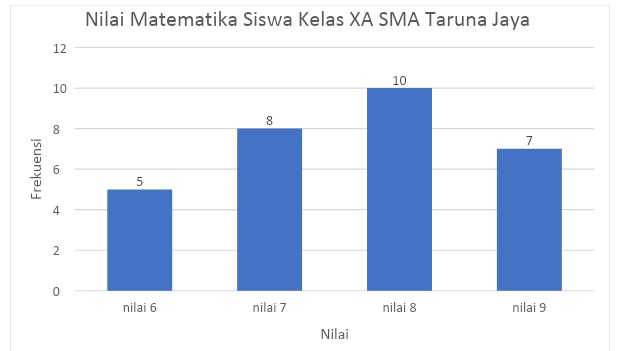
Diagram lingkaran
 

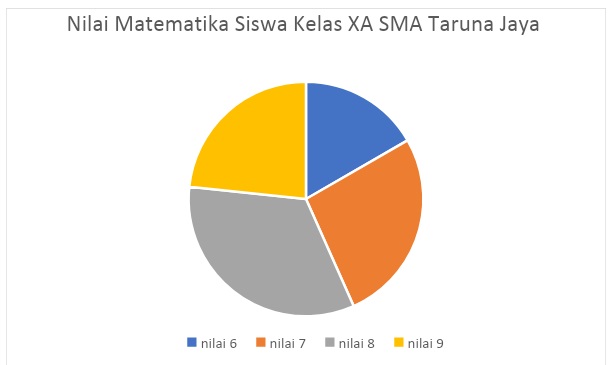
Diagram garis
 

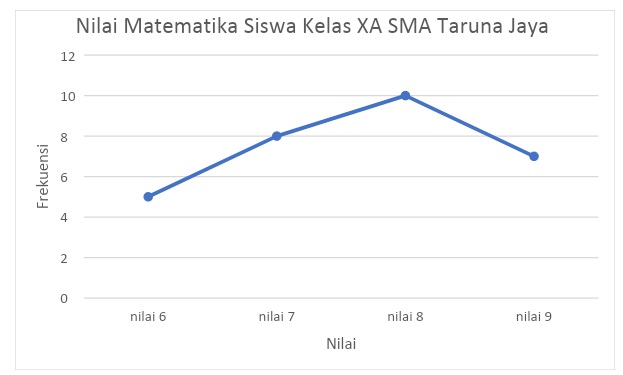
2. Pemusatan data

Pemusatan data adalah posisi kelompok data yang bisa mewakili keseluruhan data yang diperoleh pada suatu penelitian. Pemusatan data dibagi menjadi tiga, yaitu mean, modus dan median. Perbedaan antara ketiganya adalah sebagai berikut:
 
Mean (rata-rata)
 
Mean dikenal juga sebagai rata-rata. Secara matematis, mean dirumuskan sebagai berikut:
 

Modus
 
Modus adalah data yang memiliki frekuensi terbanyak. Misalnya, diketahui data 1, 1, 2, 2, 2, 2, 2, 3, 3. Modus dari data tersebut adalah 2 karena memiliki frekuensi terbanyak, yaitu 5. Secara matematis, modus dirumuskan sebagai berikut:
 
Data tunggal
 
Modus data tunggal bisa dihitung secara langsung tanpa adanya rumus tertentu.
 
Data berkelompok
 

 
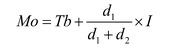
Dengan:
 
Tb = tepi bawah
d1 = selisih antara frekuensi kelas modus dan kelas sebelumnya
d2 = selisih antara frekuensi kelas modus dan kelas setelahnya
I = interval kelas.
 
Median
 
Median disebut juga sebagai nilai tengah. Untuk mencari median suatu data, kamu harus mengurutkan dahulu data tersebut mulai data terkecil hingga terbesarnya. Median dibagi menjadi dua, yaitu median data tunggal dan data kelompok.
 
Median data tunggal
 
Median data tunggal bisa kamu tentukan dengan membagi data menjadi dua bagian yang sama. Nah, data yang tepat di tengah itulah yang disebut median.
 
Median data berkelompok
 

 
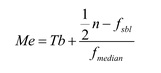
Dengan:
 
Me = median
Tb = tepi bawah
n = banyaknya data
fsbl = frekuensi sebelum frekuensi median
fmedian = frekuensi median.

3. Penyebaran data

Penyebaran data adalah besarnya penyimpangan antara sebaran data dan data pusatnya. Artinya, seberapa jauh sih perbedaan antara data pusat dan data lainnya. Ukuran penyebaran data dibagi menjadi tiga, yaitu simpangan rata-rata, ragam (varians), dan simpangan baku. Berikut ini perbedaan antara ketiganya:
 
Simpangan rata-rata
 
Simpangan rata-rata merupakan selisih mutlak antara jumlah semua nilai dan rata-ratanya.  Secara matematis, simpangan rata-rata dirumuskan sebagai berikut.
 

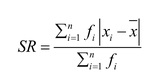
Ragam (varians)
 
Ragam merupakan ukuran penyebaran suatu data. Secara matematis, ragam dirumuskan sebagai berikut:
 

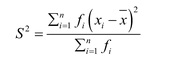
Simpangan baku
 
Simpangan baku adalah hasil pengakaran dari ragam. Namun, simpangan baku haruslah bernilai positif. Secara matematis, dirumuskan sebagai berikut.
 

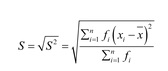
Bagaimana Penerapan Statistika Deskriptif dalam Penelitian?

Penerapan statistika deskriptif di dalam penelitian dengan mengurutkan data terlebih dahulu. Apabila data sudah diurutkan, barulah peneliti bisa menyajikannya dalam bentuk tabel, diagram, atau grafik.
 
Penyajian ini disesuaikan dengan jenis penelitian dan perolehan data. Dari tabel atau diagram tersebut, barulah bisa ditentukan ukuran pemusatan datanya. Setelah itu, peneliti bisa menentukan ukuran penyebaran datanya.

Kesimpulan

Dari pembahasan di atas dapat disimpulkan statistika deskriptif merupakan langkah pertama yang harus digunakan peneliti untuk mengolah data penelitian karena di dalamnya memuat penyajian data ukuran pemusatan data, dan ukuran penyebaran data.
 
Itulah pembahasan statistika deskriptif. Semoga membantu yaa!
 

Baca juga: Belajar Matematika: Menghitung Kemiringan atau Gradien

 
Cek Berita dan Artikel yang lain di

Google News

Viral! 18 Kampus ternama memberikan beasiswa full sampai lulus untuk S1 dan S2 di Beasiswa OSC. Info lebih lengkap klik : osc.medcom.id