Mengenal Konsep Integral: Jenis, Teknik Penyelesaian, dan Contoh Soal

Jakarta: Lingkaran menjadi salah satu bentuk pada matematika yang memiliki beberapa cara dalam menghitungnya termasuk luas dan keliling. Namun saat lingkaran membentuk bangun ruang layaknya bola, maka diperlukanlah rumus volume untuk menghitungnya. Bagaimana jika menghitung luas dan volume lingkaran? Oleh sebab itu, perlu diketahui keterkaitan luas dan volume. Integral menjadi salah satu caranya.

Pengertian Integral

Integral merupakan salah satu materi kalkulus dasar yang erat kaitannya dengan diferensial dan limit. Pada dasarnya, integral adalah kebalikan dari diferensial, sehingga disebut juga sebagai anti-turunan.
 
Dengan kata lain, rumus integral tidak berdiri sendiri, melainkan bergantung pada yang terdapat dalam turunan. Meski begitu, tak semua konsep turunan bisa diintegralkan.

Rumus Integral

Adapun rumus integral yang paling banyak digunakan hingga saat ini ialah Integral Riemann. Rumus yang ditemukan matematikawan Jerman, Georg Friedrich Bernhard Riemann, itu berbentuk sebagai berikut:
 


Keterangan:
 
A = nilai integral dari fungsi f(x)
b = batas atas variabel yang diintegrasi
o = batas bawah variabel yang diintegrasi
f(x) = fungsi yang diintegralkan
dx = variabel yang diintegrasi

Jenis jenis Integral

Integral memiliki dua jenis, yaitu integral tak tentu dan integral tentu. Lantas, seperti apa perbedaannya? Dilansir dari Zenius, berikut penjelasan mengenai jenis, teknik penyelesaian, dan contoh soal integral.

1. Integral Tak Tentu

   Integral tak tentu merupakan suatu fungsi baru yang turunannya sama seperti fungsi aslinya. Jenis integral ini tidak memiliki batas dan belum mempunyai nilai yang jelas.
    
   Nilai yang belum jelas ini dilambangkan dengan konstanta (C). Sedangkan, lambang integral tak tentu tidak mempunya batas atas dan batas bawah.

   Rumus integral tak tentu:

   

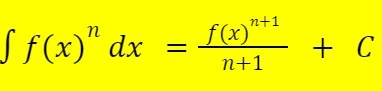
   Sifat integral tak tentu:

   
    
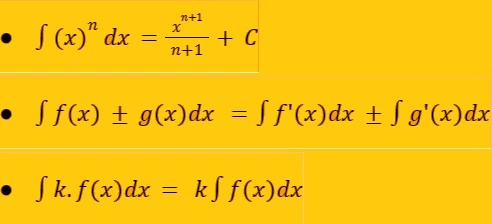
   Pengaplikasian integral jenis ini tidak hanya dalam matematika saja, tetapi juga fisika. Dalam bidang fisika, aplikasi integral tak tentu digunakan dalam konsep jarak-kecepatan-percepatan, mengetahui f(x) jika f'(x) dan f(a) diketahui, serta mengetahui f(x) bila persamaan gradien garis singgung dan titik singgung diketahui.

2. Integral Tentu

   Integral tentu adalah integral yang memiliki nilai awal dan akhir, serta batas yang jelas.
    
   Rumus integral tentu:
    
   
    
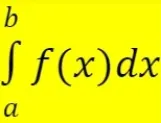
   dengan b merupakan batas atas variabel integrasi, dan a ialah batas bawah. Jika dibandingkan dengan integral tak tentu, sifat integral tentu terbilang lebih bervariatif.
    
   Sifat integral tentu: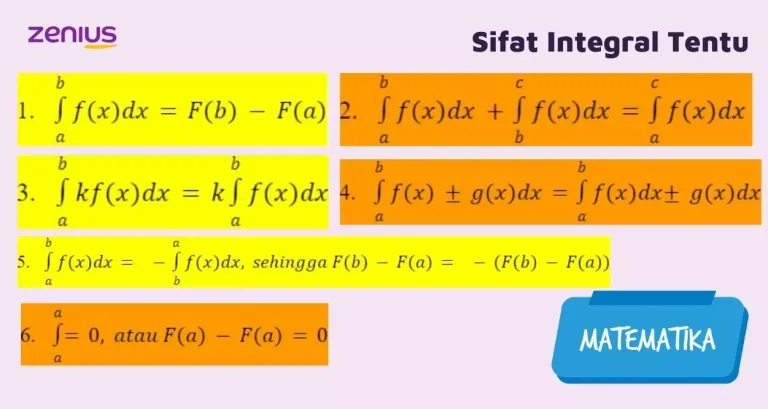
   Integral tentu biasanya diaplikasikan untuk menghitung luas daerah yang tidak beraturan dan volume benda putar.

Teknik Integral 

Dalam mengerjakan materi ini, dibutuhkan teknik atau metode untuk menyelesaikan persamaan integral. Tenik tersebut terbagi menjadi dua, yaitu teknik integral substitusi dan parsial.

1. Teknik Integral Substitusi

   Jika sebuah persamaan integral begitu kompleks, maka dibutuhkan teknik substitusi untuk menyederhanakannya. Rumus integral subtitusi adalah sebagai berikut:
    
   

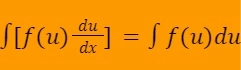
2. Teknik Integral Parsial

   Integral parsial digunakan dengan memisahkan dua fungsi berbeda, tetapi memiliki variabel yang sama. Rumus integral parsial adalah sebagai berikut:
    
   
    
   di mana f(x) = u, sehingga du = f(X)dx; dan g(x) = v, sehingga dv = g(x)dx.
    
   f(x) memiliki derajat n yang lebih besar dari 1, di mana n adalah bilangan asli. Untuk menghitungnya, pecah kedua fungsi seperti skema di bawah ini: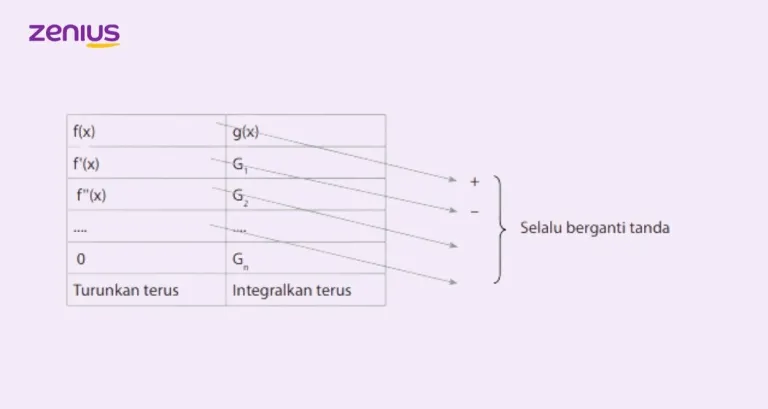

Cara menghitungnya, kali silangkan f(x) dengan G1, kemudian kali silang turunan f’(x) dengan G2, dan seterusnya. Kemudian, operasikan selang-seling hasilnya, dari positif (+), negatif (-), begitu seterusnya.
 
Dari perhitungan tersebut, diperoleh rumus sederhana sebagai berikut:
 

 
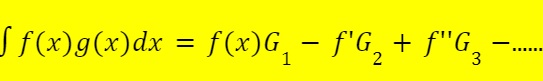
Agar lebih mudah dipahami, simak contoh soal di bawah ini:
 

Contoh soal Integral

Agar lebih mudah dipahami, simak contoh soal beserta pembahasannya berikut:
 

 

 

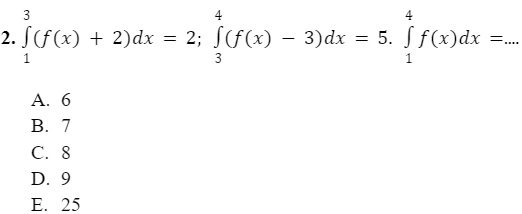
Pembahasan:

 

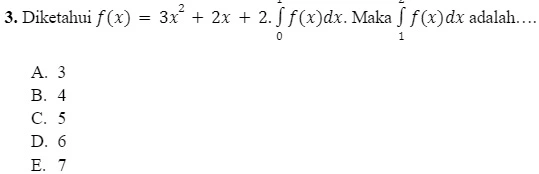
Pembahasan:

 
Itulah pembahasan mengenai konsep integral beserta jenis, teknik penyelesaian, dan contoh soal. (Nurisma Rahmatika)
 

Baca juga: Permutasi dan Kombinasi dalam Himpunan: Pengertian, Rumus, Contoh Soal

Cek Berita terbaru dan Artikel menarik lainnya di Google News
 
Cek Berita dan Artikel yang lain di

Google News

Viral! 18 Kampus ternama memberikan beasiswa full sampai lulus untuk S1 dan S2 di Beasiswa OSC. Info lebih lengkap klik : osc.medcom.id